|
Автоматические регуляторы в системах управления и их настройка
Часть 1. Промышленные объекты управления
Современные системы управления сложными промышленными объектами строятся по иерархическому принципу. Система более высокого уровня, исходя из общего алгоритма управления, выдает команды на включение или отключение отдельных локальных объектов, а также осуществляет выбор частных критериев управления этими объектами. Локальные системы управления осуществляют поддержание заданных режимов, как в пусковых, так и в нормальных эксплуатационных условиях. Количество регулируемых параметров в отдельно взятой локальной системе управления обычно невелико и составляет один-два параметра. Из общего числа систем управления современным производством локальные системы составляют около 80%. Качество работы локальных систем управления во многом определяет стабильность и качество выходного продукта.
Классификация объектов управления
По характеру протекания технологических процессов объекты управления делятся на циклические, непрерывно-циклические и непрерывные. Локальные системы наиболее широко применяются для управления объектами двух последних типов.
По характеру установившегося значения выходной величины объекта при действии на его вход ступенчатого сигнала выделяют объекты с самовыравниванием и без него.
По количеству входных и выходных величин и их взаимосвязи объекты делятся на одномерные (один вход и один выход) и многомерные. Последние могут быть многосвязными — когда наблюдается взаимное влияние каналов регулирования друг на друга, либо несвязные — взаимосвязь между каналами которых мала.
По виду статических характеристик объекты делятся на линейные и нелинейные. В последних статическая характеристика может быть гладкой, линеаризуемой в окрестности заданной точки, либо может носить существенно нелинейный характер. Большинство систем регулирования относится к классу систем автоматической стабилизации режима работы объекта относительно его рабочей точки. В этом случае отклонения переменных относительно рабочей точки малы, что позволяет использовать линейные модели объекта управления. Для системы автоматической стабилизации не обязательно определение полной статической характеристики объекта — достаточно знать лишь динамический коэффициент усиления в окрестности рабочей точки.
Реальные объекты занимают в пространстве какойлибо объем, поэтому регулируемая величина зависит не только от времени, но и от текущих координат точки измерения. Поэтому положение объекта управления описывается системой дифференциальных уравнений в частных производных. При использовании точечного метода измерения с одним датчиком система дифференциальных уравнений в частных производных переходит в систему уравнений с обычными производными. Это существенно упрощает построение математической модели объекта при определении его передаточной функции. Однако при наличии множества датчиков и исполнительных механизмов может возникнуть необходимость использования множества управляющих сигналов (распределенное управление).
В зависимости от интенсивности случайных возмущений, действующих на объект, они делятся на стохастические и детерминированные. В реальных условиях часто точно неизвестны ни точка приложения возмущения F, ни его характер.
Известно, что лишь при наличии достаточно точной математической модели объекта можно спроектировать высококачественную систему управления этим объектом, причем, согласно принципу Эшби, сложность управляющего устройства должна быть не ниже сложности объекта управления. Поэтому основной целью построения математической модели объекта управления является определение структуры объекта, его статических и динамических характеристик. Особенно важно определение структуры для многомерных и многосвязных объектов управления. В тоже время для локальных объектов управления определение структуры может быть сведено к определению порядка дифференциального уравнения, описывающего объект. Кроме того, оцениваются входные сигналы и возмущения, действующие на объект (их статистические характеристики, точки приложения, максимальные амплитуды). Значение этих характеристик позволяет выбрать структуру регулятора и рассчитать параметры его настройки, ориентируясь на критерий качества работы этой системы.
Наряду с динамической частью W(p) в структуре объекта могут содержаться различные запаздывания в сигналах управления, измерения и состояния (рецикла)(рис.1).
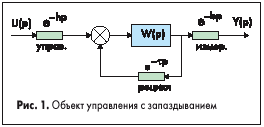
Наличие запаздывания объясняется конечной скоростью распространения потоков информации в объектах. Наряду с этим при понижении порядка модели объекта вводят дополнительное динамическое запаздывание. Для этого выделяют одну наибольшую постоянную времени,а все остальные малые постоянные времени заменяют звеном динамического запаздывания.
Методы получения математического описания
Применяются аналитические, экспериментальные и комбинированные методы получения математического описания объектов управления.
Аналитические методы базируются на разработке уравнений, описывающих физикохимические и энергетические процессы, протекающие в исследуемом объекте управления. В настоящее время для многих классов объектов управления получены их математические модели. При получении таких описаний обычно оперируют с дифференциальными уравнениями в частных производных.
Экспериментальные методы предполагают проведение серии экспериментов на реальном объекте управления. По результатам экспериментов оценивают параметры динамической модели объекта, предварительно задавшись ее структурой.
Наиболее эффективны комбинированные методы построения математической модели объекта, когда используют аналитически разработанную структуру объекта, а ее параметры определяют в ходе натурных экспериментов.
Аналитические методы
Достоинства аналитических методов:
- позволяют определить математическое описание еще на стадии проектирования системы управления;
- позволяют учесть все основные особенности динамики объекта управления, такие, как наличие нелинейностей, нестационарность, распределенные параметры и т.д.;
- обеспечивают получение универсального математического описания, пригодного для широкого класса аналогичных объектов управления.
Недостатки:
- трудность получения достаточно точной математической модели, учитывающей все особенности реального объекта;
- проверка адекватности модели и реального процесса обычно требует проведения натурных экспериментов;
- многие математические модели имеют ряд трудно оцениваемых в численном выражении параметров.
Методы экспериментального определения динамических характеристик объектов управления
В настоящее время при расчете настроек регуляторов локальных систем широко используются достаточно простые динамические модели промышленных объектов управления. Например, использование моделей инерционных звеньев первого или второго порядка с запаздыванием для расчета настроек регуляторов обеспечивает, в большинстве случаев, качественную работу реальной системы управления. В связи с этим возникает задача определения численных значений параметров динамических моделей промышленных объектов управления. Опыт показывает, что значительно проще определить эти параметры экспериментально на реальном объекте управления. Особенно оправдан такой подход для одномерных объектов управления, работающих совместно с системой автоматической стабилизации.
В зависимости от вида переходной характеристики (кривой разгона) задаются чаще всего одним из трех видов передаточной функции объекта управления:
- В виде передаточной функции инерционного звена первого порядка
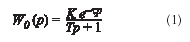
где K, T,t — коэффициент усиления,постоянная времени и запаздывание, определенные в окрестности номинального режима работы объекта.
- Более точно динамику объекта описывает модель второго порядка с запаздыванием
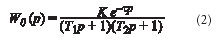
- Для объекта управления без самовыравнивания передаточная функция имеет вид
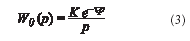
Экспериментальные методы определения динамических характеристик объектов управления делятся на два класса:
- Методы определения временных характеристик объекта управления.
- Методы определения частотных характеристик объекта управления.
Временные методы определения динамических характеристик делятся, в свою очередь, на активные и пассивные.
Активные методы предполагают подачу на вход объекта тестовых сигналов, каковыми являются:
- регулярные функции времени (ступенчатый перепад или прямоугольный импульс, гармонический сигнал, периодический двоичный сигнал);
- сигналы случайного характера (белый шум, псевдослучайный двоичный сигнал).
зависимости от вида тестового сигнала выбирают соответствующие методы обработки выходного сигнала объекта управления. Так,например, при подаче ступенчатого перепада снимают кривую разгона объекта, а при подаче прямоугольного импульса снимают кривую отклика (применяется для объектов, не допускающих подачу на вход объекта ступенчатых сигналов).
Достоинствами активных методов являются:
- достаточно высокая точность получения математического описания;
- относительно малая длительность эксперимента.
Следует учитывать, что активные методы в той или иной степени приводят к нарушению нормального течения процесса.
В пассивных методах на вход объекта тестовые сигналы не подаются, а лишь фиксируется естественное поведение объекта в процессе его нормального функционирования. Полученные реализации массивов данных входных и выходных сигналов обрабатываются статистическими методами. По результатам обработки получают параметры передаточной функции объекта. Однако такие методы имеют ряд недостатков:
- малая точность получаемого математического описания (так как отклонения от нормального режима работы малы);
- необходимость накопления больших массивов данных с целью повышения точности;
- если эксперимент проводится на объекте, охваченном системой регулирования, то наблюдается эффект корреляции между входным и выходным сигналами объекта через регулятор, что снижает точность математического описания.
Определение динамических характеристик объекта управления по кривой его разгона
При определении динамических характеристик объекта по кривой его разгона на вход подается или ступенчатый сигнал или прямоугольный импульс. Во втором случае кривая отклика должна быть достроена до соответствующей кривой разгона.
При снятии кривой разгона необходимо выполнить ряд условий:
- Если проектируется система стабилизации, то кривая разгона должна сниматься в окрестности рабочей точки процесса.
- Кривые разгона необходимо снимать как при положительных, так и отрицательных скачках управляющего сигнала. По виду кривых можно судить о степени асимметрии объекта. При небольшой асимметрии расчет настроек регулятора рекомендуется вести по усредненным значениям параметров передаточных функций, а линейная асимметрия наиболее часто проявляется в тепловых объектах управления.
- При наличии зашумленного выхода желательно снять несколько кривых разгона с их последующим наложением друг на друга и получением усредненной кривой.
- При снятии кривой разгона необходимо выбирать наиболее стабильные режимы процесса, когда действие случайных внешних возмущений маловероятно.
- При снятии кривой разгона амплитуда тестового сигнала должна быть, с одной стороны, достаточно большой, чтобы четко выделялась кривая разгона на фоне шумов, а с другой стороны, она должна быть достаточно малой, чтобы не нарушать нормальной работы объекта.
Сняв кривую разгона и оценив характер объекта управления (с самовыравниванием или без), можно определить параметры соответствующей передаточной функции. Например, передаточную функцию вида (1) рекомендуется применять для объектов управления с явно выраженной доминирующей постоянной времени (одноемкостный объект). Перед началом обработки кривую разгона рекомендуется пронормировать (диапазон изменения нормированной кривой 0 –1) и выделить из ее начального участка величину чистого временного запаздывания.
Рассмотрим нормированную кривую разгона объекта, у которой заранее выделена величина чистого запаздывания t 3 =3 мин. Построим график кривой разгона (рис.2) по ее значениям, приведенным в таблице 1.
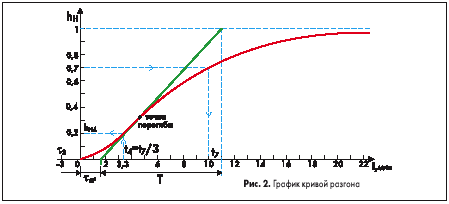
Таблица 1
| 2 |
4 |
6 |
8 |
10 |
12 |
14 |
| 0,087 |
0,255 |
0,43 |
0,58 |
0,7 |
0,78 |
0,84 |
Динамический коэффициент усиления K объекта определяется как отношение приращения выходного сигнала к приращению входного в окрестности рабочей точки.
Определение динамических характеристик объектов по кривой разгона можно производить двумя методами.
- Метод касательной к точке перегиба кривой разгона. В данном случае точка перегиба соответствует переходу кривой от режима ускорения к режиму замедления темпа нарастания выходного сигнала. Постоянная времени Т и динамическое запаздывание t d определяются в соответствии с графиком рис.2, то есть t =t 3 +t d .
- Формульный метод позволяет аналитически вычислить величину динамического запаздывания и постоянной времени по формулам
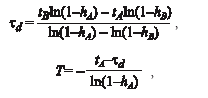
где значение h A берется в окрестности точки перегиба кривой, а значение h B принимается равным 0,8 –0,85.По этим значениям определяются и моменты времени t A и t B .
Методику определения параметров динамической модели (3) объекта без самовыравнивания рассмотрим на примере кривой разгона уровня в барабане котла теплоагрегата. Предполагается, что на вход объекта увеличили подачу воды на 10 т/час =.G, при этом уровень начал увеличиваться. Приращение уровня зафиксировано в таблице 2.
Таблица 2
| t c ,сек |
0 |
100 |
200 |
300 |
| Dh,мм |
0 |
20 |
76 |
135 |
График разгонной характеристики объекта без самовыравнивания, построенной в соответствии с приведенной таблицей, показан на рис.3.
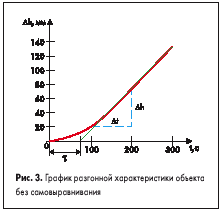
Для объекта без самовыравнивания коэффициент усиления определяется как отношение установившейся скорости изменения выходной величины к величине скачка входного сигнала. В нашем примере
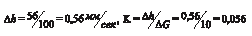
Величина динамического запаздывания определяется так, как показано на рис.3.
Метод Орманса
Это метод позволяет по нормированной кривой разгона определить две доминирующие постоянные объекта управления для модели вида (2).
Методика поясняется с использованием предыдущей кривой разгона, приведенной на рис.2. Для этого:
- Из нормированной кривой разгона определяется время, соответствующее значению h H =0,7 и обозначается t 7 . Из точки t 4 =t 7 /3 поднимается перпендикуляр до кривой разгона и определяется величина h H4. Аналитически доказана связь между точками кривой разгона и параметрами модели, а именно t 7 =1,2 (T 1 +T 2 ).
Постоянные времени объекта управления T 1 и T 2 определяются с помощью вспомогательной величины Z2, для нахождения которой используется номограмма (рис.4).
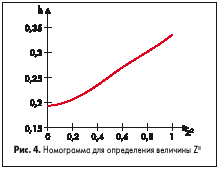
Постоянные времени объекта управления T 1 и T 2 определяются по следующим формулам:
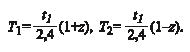
Если h H4 <0,19, то для определения динамики объекта используют метод площадей. Если T 1 >>T 2, то можно перейти к модели первого порядка.
Частотные методы определения динамических характеристик
Эти методы предполагают, что на вход объекта подается периодический сигнал с известной частотой и амплитудой. При этом, если этот сигнал формируется с помощью меандра, то эквивалентная амплитуда синусоидального сигнала будет больше амплитуды прямоугольного импульса в 4/p раза, что должно учитываться при расчете частотных характеристик. Модуль амплитудно-фазовой характеристики определяется как отношение амплитуды выходной гармоники к амплитуде входной. Фазовая характеристика характеризует сдвиг фаз между этими гармониками на различных частотах пробного сигнала. Эти характеристики могут определяться непосредственно по графикам входного и выходного сигналов объекта, либо методом синхронного детектирования.
Частотные методы определения динамических характеристик объекта предполагают наличие двух этапов, на которых определяются:
- Амплитудно-фазовая характеристика объекта.
- Передаточная функция объекта.
Амплитудно-фазовая характеристика (АФХ) объекта несет б o льшую информацию об объекте, чем его кривая разгона. Таким образом, определение динамики объекта управления по его АФХ позволяет получить более точную динамическую модель, работающую в широком диапазоне частот.
В процессе проведения экспериментов по снятию АФХ желательно предварительно определить так называемый существенный диапазон частот объекта. Для этого необходимо найти критическую частоту колебаний W(p)объекта, то есть частоту, на которой входная и выходная гармоники находятся в противофазе.
Для экспериментального определения частоты W(p)рекомендуется использовать метод двухпозиционного регулирования неполным притоком. Рабочий диапазон частот эксперимента (6 –7 точек) выбирается из соотношения:w =(0,5 –2,5)w к.
По виду полученной в результате построения АФХ выбирается нужный вид передаточной функции объекта управления.
На втором этапе необходимо определить параметры модели объекта так, чтобы АФХ модели как можно точнее соответствовала АФХ реального объекта.
При наличии нелинейной статической характеристики объекта управления при подаче на его вход тестовых воздействий выходной сигнал объекта может отличаться от синусоидального. В этом случае для выделения истинного значения амплитуды первой гармоники рекомендуется использовать метод двенадцати ординат.
Определение параметров объекта управления методом наименьших квадратов
Этот метод предполагает, что используются массивы значений входных и выходных сигналов объекта, снятых через некоторый интервал времени Т К — период квантования. Во входном сигнале объекта должна присутствовать как постоянная, так и тестовая составляющие. Постоянная составляющая определяет положение рабочей точки процесса, в окрестности которой и производится определение параметров динамической модели объекта. Учитывая, что используются дискретные значения входных и выходных значений, необходимо работать с дискретными моделями объекта.
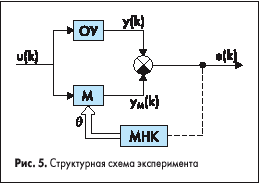
Рассмотрим методику применения метода наименьших квадратов на примере цифровой модели первого порядка, заданной в виде:
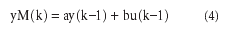
Структурная схема эксперимента с использованием модели объекта показана на рис.5. Здесь ОУ — объект управления, М — модель объекта, u(k), y(k), e(k), yM(k),q — входной и выходной сигналы, текущая ошибка идентификации, выходной сигнал модели и вектор оценки параметров.
Пусть накоплено N+1 точек измерения входного и выходного сигналов объекта. В методе наименьших квадратов обобщенная ошибка идентификации должна быть минимальна:

Для упрощения записи опустим в дальнейших выкладках пределы суммирования.Раскроем выражение (5)в виде
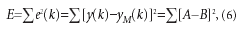
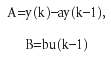
После соответствующих преобразований формулы (6), раскрытия скобок и приведения подобных получим
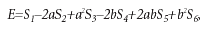
где
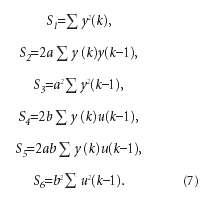
При минимизации E необходимо определить частные производные по параметрам a и b.
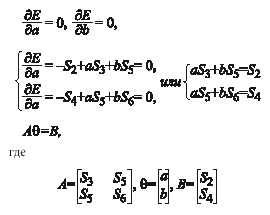
Откуда следует формула для вычисления оценок вектора параметров объекта управления по методу наименьших квадратов

Обратная матрица A–1 всегда существует, так как исходная матрица A симметрична и положительно определенна, что следует из формул (7).
Зная параметры дискретной модели, можно определить параметры передаточной функции объекта
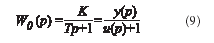
Известно, что связь между параметрами дискретной модели (4) и передаточной функции (9) определяется формулами
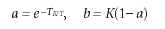
Откуда следует, что
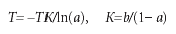
При использовании МНК получаемые оценки вычисляются с некоторыми ошибками, которые называются смещением оценок. Для получения достаточно представительных результатов необходимо выполнить ряд условий:
- Подавать на вход объекта управления какой-либо тестирующий сигнал, достаточно богатый в спектральном отношении (например, псевдослучайную двоичную последовательность). Такой сигнал эквивалентен подаче на вход объекта множества гармонических составляющих, что позволяет оценить большую полосу частот АФХ объекта.
- Объем исследуемой выборки (N) должен быть достаточным для получения представительных оценок, причем, чем меньше уровень тестового сигнала, тем больше должно быть число N. Существует рекуррентный метод наименьших квадратов, который позволяет в реальном времени получать текущие оценки параметров объекта и по их сходимости определить величину N и момент окончания эксперимента.
- С увеличением уровня шумов на выходе объекта точность оценок снижается. Смещение оценок возникает и при охвате исследуемого объекта обратной связью через регулятор, так как в этом случае возникает корреляционная связь между входом и выходом объекта,приводящая к смещению оценок.
Учет запаздывания в объекте управления приводит к появлению задержки в управляющем сигнале на М периодов квантования
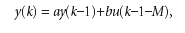
где M =int(t /T K )В связи с этим, наряду с оценкой параметров a и b необходимо определить и величину задержки M. Это можно сделать при нахождении глобального минимума обобщенной ошибки идентификации E для различных величин задержки M =0ёM max , используя один и тот же массив данных.
За основу публикации взят курс лекций, читаемый профессором В.М.Мазуровым на кафедре АТМ Тульского государственного университета
|